| |
Fourier Series
A Fourier series is an expansion of a function in a series of sines and cosines such as
One advantage of a Fourier representation over some other representations, such as a Taylor series, is that it may represent discontinuous functions. Two well known examples of such functions are the square wave and the sawtooth wave, both are very useful in electronic circuits that handle pulses. The Fourier representation of a square wave is given by
namely, the cosine terms have vanished, and only the odd terms in the sine series remain. The coefficients in this case are 1/n for the odd terms and 0 for the even terms.
The Fourier representation of a sawtooth wave is given by
Here again, the cosine terms have vanished. The coefficients in this case are 1/n for the the odd terms and -1/n for the even terms.
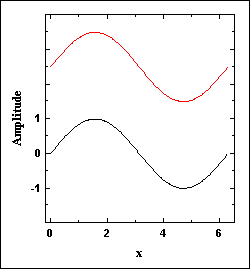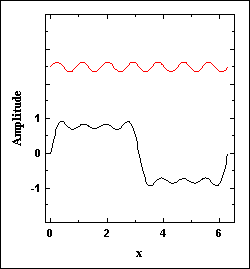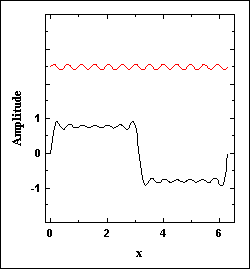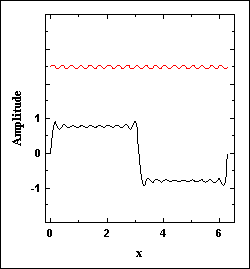
The following graphs show how a square wave and a sawtooth wave are built as sums of sine waves. The upper traces (in red) are the terms added to the sum on each cycle. Note how each added term gets us closer to the desired wave form.
 |
 |
| Figure 1. A square wave |
Figure 2. A sawtooth wave |
|
|
