Demos
Code
using the Levenberg-Marquardt method
In this demonstration we use a simulated data signal and fit to it a sum of three Gaussians. Each Gaussian may have any amplitude, position, and width. The data is created by taking a specific signal of three Gaussians and adding to it random noise.
Figure 1 displays the simulated data (in red) and the fitted curve (in black). When the program is running we can see the process of finding the best fit in action.
 |
| Figure 1. Data (red dots) and fitted curve (solid black) |
It is interesting to see how close we get to the original signal which was used to create the simulated data, so in Fig. 2 we show this theoretical curve (red) together with the fitted curve (black).
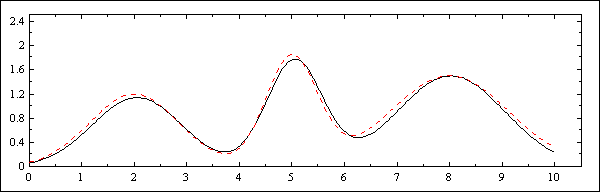 |
| Figure 2. Theoretical (dashed red) and fitted (solid black) curves. |
And finally, the quality of the fit is determined by the value of X 2 and the covariance matrix. These are presented below. The covariance matrix is represented by the mean value of its diagonal elements (which give the variance of each fitted parameter), and by their standard deviation: